[原创][数学] 步步推导不用计算机算平方根的公式（笔算开平方）

笔者有段时间很疯迷于数学，12岁那段时间是高峰期，曾经出国比赛，但是最近“转行”到电脑了，数学也很少去理它了。
今天在整理书橱的时候，找到了一篇蛮有意义的手稿，应该是笔者12岁那年写的，里面是一些关于“笔算开平方”的一些研究与公式推导。由于那个时候不太成熟、学的东西也不会很多，研究的那些资料遇到很多的困难，只是初步的推了一些公式，花了一整天来重新整理，才明白里一些原理与推导的方法，于是就步步研究，写了起来，然后又怕忘记，所以特此写了这篇文章，就当作备份吧。
温馨提醒：如果你很讨厌数学，请不要在看下去了，这篇文章会把你的头脑炸晕的！
“笔算开平方”是什么呢？举个例子来说，比如有天开始，你忘了带计算机，考题要你算一个数的平方根（square root），况且你不能与人家借计算机的情况下，要怎么样开平方呢？另一种情况就是，你有计算机，但是却没有带开平方根的功能，只有简单的加减乘除，要如何算平方根呢？
你有两种方法：1、就是一点一点的试 2、投机取巧，根据一些恒等式，将复杂的开方转换成简单的加减乘除。
其实这个方法在网上已经有了，比如较出名的“牛顿法”，这种方法巧妙与：就算你取的初始值是个错误的值，这个公式的输出会知道调整到正确的值（也就是说该数的平方根）
笔者的方法是根据与恒等式：

而我们设 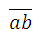 b为一个数的最后一位数，a则是整个数除了最后一位数之外的数
举例来说，我们的数为123456，则
所以我们有 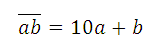，而
现在我们知道 （也就是说，我们知道 的值，我们要找a和b的值）是什么了，我们要倒推回去，我们要知道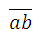的值，这就是开平方（square root..）
在笔算开平方时，a是我们已经计算出来的结果，而b是当前需要计算的为上的数，而r为相减剩下来的数（当r=0时，就代表该数是个完全平方数），如图下所示：




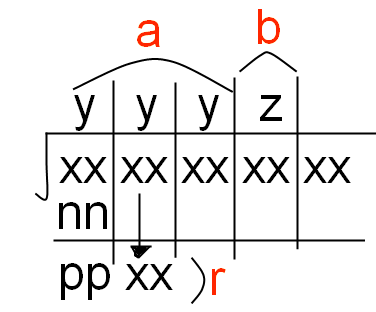
每次估算下一位数时， 中的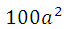 会被减掉，剩下
设我们现在需要估算的位数为 ，而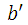 必须满足以下不等式：

当中，r为相减后剩下来的“余数”
的值，可以以以下公式估算出：

如上图所示，有时候估算出的 ，会大于9，所以我们让 等于9就是了。
好吧，然我们举个例子来更详细的表达出笔算开平方的具体步骤
首先我们选一个数，这里就然他为200吧
然后以2位为一组分开：

先来估算第一位数，很显然的 ，所以第一位就是1了

，然后脱下两个0，和之前的1合并起来，成为100
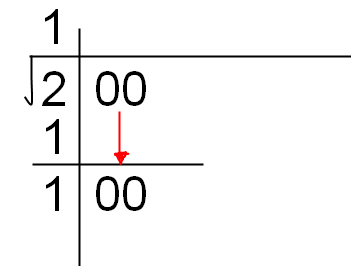
这一步，我们要用到我们的估算公式来估算下一位的位数
现在，

但是 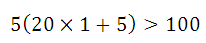，所以让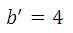 ，不等式就会成立：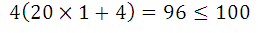

下一位就是4，我们可以补上多余的0：

我们可以一直重复上述步骤，以求得接下来一位：














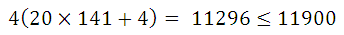
一直继续下去，就会得到：

之前我说过 有时候会大于9，距离来说，我们以899为例子：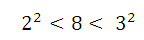






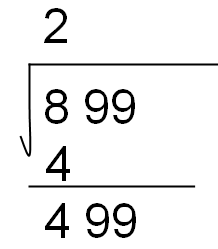
继续下去就可以得到：

这个笔算开平方可以以不同次方的恒等式来推导出笔算开n次方的方法，笔者试过推导开立方的方法，但是估算下一位的数有点麻烦（功力不好啊）